
Revista Cubana de Ciencias Forestales. 2021; enero-abril 9(1): 124-139
Factor y cociente de forma preliminar de Brachystegia floribunda Benth.
Preliminary form and quotient factor of Brachystegia floribunda Benth.
Fator de forma preliminar e quociente de forma de Brachystegia floribunda Benth.
Edilio Aldana Pereira1*![]() https://orcid.org/0000-0001-8891-9799
https://orcid.org/0000-0001-8891-9799
Yordan Lores Pérez2![]() https://orcid.org/0000-0002-8252-4590
https://orcid.org/0000-0002-8252-4590
1Universidad de Pinar del Rio "Hermanos Saíz Montes de Oca". Pinar del Río, Cuba.
2Universidad de Guantánamo, Cuba.
*Autor para la correspondencia: aldana@pap.upr.edu.cu
Recibido:17/7/2020.
Aprobado:11/12/2020.
RESUMEN
Brachystegia floribunda Benth es una de las especies de mayor importancia y uso del bosque natural de Miombo, del Planalto Central de Angola, encontrándose mezclada con otras especies también importantes de los géneros Brachystegia, Isoberlínea y Julbernardia, entre otros, pero ocupando el mayor porcentaje de la superficie forestal; no obstante, el conocimiento veraz referente a las estimaciones de su volumen comercial es limitado. Esta investigación, ejecutada en las áreas forestales de la formación de Miombo, tuvo como objetivo, determinar los factores de forma del fuste y ramas, así como el cociente de forma o factor diamétrico del fuste. Se empleó una muestra de 53 árboles, derribados para aprovechamiento forestal y cubicado rigurosamente. Se determinó el factor volumétrico de forma, con y sin agrupamiento de los árboles en clases de diámetros. Para las ramas, solo se determinó el factor volumétrico de forma, con y sin agrupamiento, en clases de longitud de las mismas. Como resultado final se concluye que el factor volumétrico y diamétrico de forma del fuste tienen mejor correlación con el diámetro, agrupados en clases; y la correlación del factor volumétrico de las ramas es mayor cuando se agrupan en clases de longitud.
Palabras clave: Estimaciones; Volumétricas; Factor de forma; Cociente de forma; Brachystegia floribunda.
ABSTRACT
One of the most important and widely used species in the natural forest of Miombo, in the Central Highlands of Angola, Brachystegia floribunda Benth is found mixed with other important species of the genera Brachystegia, Isoberlínea and Julbernardia, among others, but occupying the largest percentage of the forest area; however, there is limited accurate knowledge regarding the estimation of its commercial volume. This research, carried out in the forest areas of the Miombo formation, had the objective of determining the shape factors of the trunk and branches, as well as the shape quotient or diametric factor of the trunk. A sample of 53 trees, felled for logging and rigorously cubed, was used. The volumetric shape factor was determined, with and without grouping the trees in diameter classes. For the branches, only the volumetric shape factor was determined, with and without grouping, in branch length classes. As a final result, it was concluded that the volumetric and diameter shape factor of the trunks had a better correlation with the diameter, grouped in classes; and the correlation of the volumetric shape factor of the branches was higher when grouped in length classes.
Keywords: Volumetric estimate; Form factor; Form quotient; Brachystegia floribunda.
RESUMO
Brachystegia floribunda Benth é uma das espécies mais importantes e utilizadas na floresta natural de Miombo, no planalto central de Angola, misturada com outras espécies importantes dos géneros Brachystegia, Isoberlínea e Julbernardia, entre outros, mas ocupando a maior percentagem da área florestal; no entanto, o verdadeiro conhecimento sobre as estimativas do seu volume comercial é limitado. Esta investigação, realizada nas zonas florestais da formação Miombo, teve como objetivo determinar os fatores de forma do tronco e dos ramos, bem como o quociente de forma ou o fator diamétrico do tronco. Foi utilizada uma amostra de 53 árvores, abatidas para abate e rigorosamente cortadas em cubos. O fator de forma volumétrica foi determinado, com e sem agrupamento das árvores em classes de diâmetro. Para os ramos, apenas foi determinado o fator de forma volumétrica, com e sem agrupamento, em classes de comprimento. Como resultado final, conclui-se que o fator volumétrico e o diâmetro do tronco têm uma melhor correlação com o diâmetro, agrupados em classes; e a correlação do factor volumétrico dos ramos é maior quando são agrupados em classes de comprimento.
Palabras chave: Estimativas; Volumétrica; Factor de forma; Quociente de forma; Brachystegia floribunda.
INTRODUCCIÓN
Brachystegia floribunda Benth es conocida vulgarmente por ossasa y también por sassa en otras regiones de Angola (Sanfilippo, 2014). Es un árbol cuyo tronco es recto y cilíndrico, de 6 -19 cm de diámetro en la base, utilizado, principalmente, en la producción de carbón de buena calidad, leña, construcción de viviendas y objetos de arte de madera.
El bosque abierto de Miombo ocupa cerca de 45,2 % de la superficie forestal total de Angola, dispersándose por vastas zonas del país y presenta innumerables asociaciones dominantes, la más frecuente está constituida por los géneros Isoberlínea, Brachystegia y Julbernardia; Brachystyergia speciformis, Brachystegia tamarindoides, Brachystyergia floribunda, Brachystegia boehmii, Brachystegia utilis, Julbernardia paniculata y Ficus sansibarica.
La formación de Miombo es de media productividad en términos de madera comercial, mas, tiene un alto valor social en términos de combustible leñoso, materias de construcción, productos alimenticios y plantas medicinales (Caetano 2012). Varios autores han realizado trabajos de investigación en esta formación de bosque (Diniz 1973, Van Wyk 2013, Sardinha 2008, Figueiredo y Smith 2014, Sanfilippo 2013).
Brachystegia floribunda Benth. constituye el objeto del presente trabajo de investigación. Según Péllico (2004) existe amplia información sobre la volumetría de árboles basada en método matemático. Las ecuaciones volumétricas constituyen uno de los procedimientos más eficientes en la estimación de volumen en árboles en pie. No siempre las ecuaciones se ajustan a todas las especies forestales y condiciones de las poblaciones forestales, siendo recomendable probarlas y elegirse el modelo de mejor resultado (Thomas 2006).
Si el volumen de un árbol es determinado correctamente, el valor encontrado es válido para otro árbol de igual diámetro, altura y forma (Thiersch et al., 2006).
El volumen real de un árbol es el porcentaje del volumen de un cilindro, cuya definición se da por el diámetro a altura de 1,3 m del suelo y por la altura total o comercial de los árboles. Así, esa relación entre los volúmenes es llamada factor de forma. Según el mismo autor, el volumen de un árbol puede ser estimado multiplicándose el volumen cilíndrico por un factor de forma medio apropiado para la especie.
Existe poca información sobre investigaciones de factores volumétricos y diamétricos de forma del fuste para especies latifoliadas, sean naturales o plantadas.
Por tanto, el problema científico de esta investigación está relacionado con la ausencia casi total de informaciones dendrométricas y dasométricas de las principales especies forestales de Miombo. De ahí la necesidad de comenzar la investigación en el tema relacionado con la forma del fuste, en la especie objeto de estudio.
El objetivo es determinar los factores volumétrico y diamétrico de forma del fuste y ramas, así como la validación de los mismos en la especie Brachystegia floribunda.
MATERIALES Y MÉTODOS
En total se derribaron y cubicaron rigurosamente 66 árboles, de los cuales fueron utilizados 53, para el cálculo de los factores y cocientes de forma, y 13 se emplearon para la validación de los resultados obtenidos.
La variable diámetro fue medida en la base del fuste, a 0,3 m, a 0,5 m, a 1,3 m, a 1,5 m y a partir de esta medida, hasta el final, a cada 0,5 m. Otras variables medidas fueron: altura total del árbol, altura comercial hasta la base de la copa (fuste) y el diámetro a la mitad de la longitud total (d0.5H). También se realizaron las mismas mediciones en las ramas de los árboles, pero en la base de la rama (db), a 0,3 m (d0,3) y a 1 m(d1,0) y de aquí a 0,5 m hasta el final de la rama y, además, se midió el diámetro en la mitad de la longitud de la rama (Figura 1).
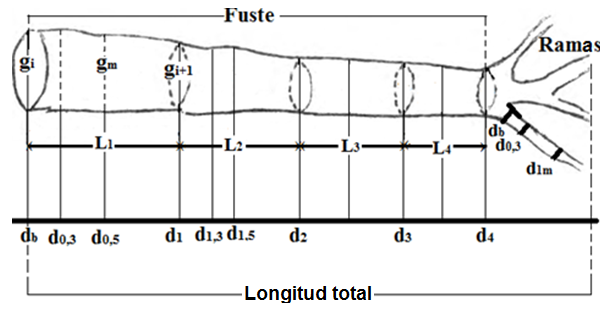
Figura 1. - Esquema de la medición de diámetros en el árbol derribado
El método utilizado fue el de secciones absolutas, y el volumen se calculó a través de la fórmula descrita por Newton (Ecuación 1):
![]()
Donde:
Vi = Volumen de la sección i;
gi = Área de la sección del extremo mayor;
gm = Área en la mitad de la sección;
gi+1 = Área de la sección del extremo menor;
Li = Longitud de la sección.
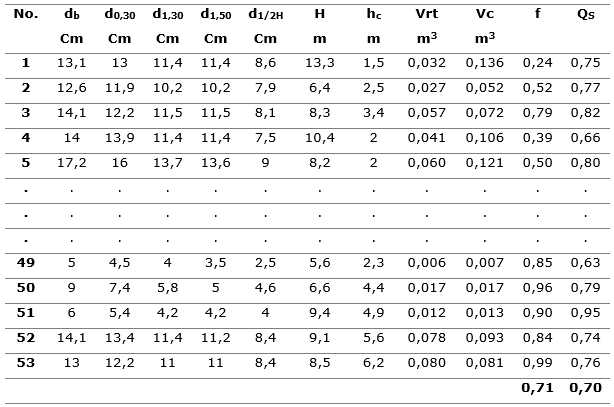
Las bases de datos donde se registran las variables dendrométricas con corteza, obtenidas para el fuste y ramas respectivamente de los 53 árboles muestreados están en el archivo personal de los autores. En la Tabla 1, sólo se muestra un esquema de la base de datos con algunos valores.
Tabla 1. - Base de datos del fuste con corteza de los 53 árboles muestra de Brachystegia florinunda
Para el cálculo del factor de forma fue utilizada la ecuación (Ecuación 2) y (Ecuación 3):
![]()
![]()
Para el cálculo del cociente de forma o factor diamétrico de forma se empleó el método de Schiffel, o sea (Ecuación 4):
![]()
Donde:
d(1/2h) = Diámetro a la mitad de la altura del árbol;
d1.3= diámetro a 1,3 m del suelo;
Qs = cociente de forma de Schiffel.
Así, la estimación del volumen será (Ecuación 5):
![]()
Donde:
DAP = d1.3;
h = altura del árbol;
Qs = cociente de forma de Schiffel.
Para determinar los estadísticos de validación se utilizó principalmente el coeficiente de determinación (R2), el error estándar de la estimación (EEE). Estos estadísticos se estimaron como sigue (Ecuación 6).
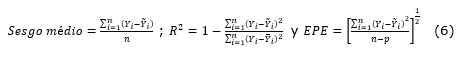
Donde:
Y1 = valor observado o la variable dependiente;
Y1 = valor medio de los datos observados;
Y1 = valor predictivo
p = número de parámetros del modelo incluyendo la intercepción.
RESULTADOS Y DISCUSIÓN
En las dos últimas columnas de la Tabla 1 están los valores medios del factor de forma con corteza para árboles individuales de B. floribunda y en la última fila aparecen los valores medios del factor volumétrico de forma f1,3=0,71 y el factor diamétrico de forma QS=0,70. Prácticamente no hay deferencia entre ambos factores. Como se muestra en la Figura 2, el factor volumétrico de forma tiene una tendencia decreciente leve respecto al aumento de los diámetros.
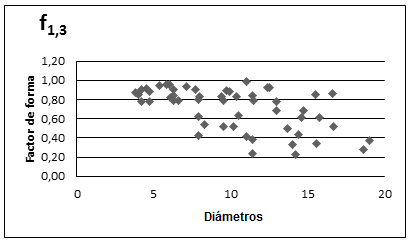
Figura 2. - Correlación del factor de forma respecto al diámetro de los árboles
Se analizó la tendencia de la correlación f1,3/d1,3 con 5 tipos de ecuaciones de correlación (logarítmica, lineal, potencial, exponencial y polinómica) con los datos individuales de los árboles muestreados sin ningún tipo de agrupamiento. En todas las ecuaciones hay una tendencia decreciente de f1,3 respecto a los diámetros, pero el coeficiente de determinación (R2) es muy bajo, aunque la mayor correlación la muestra la ecuación lineal con un R2 = 0,3176 y la polinómica de segundo grado con un R2=0,3181 (ver Figura 3).
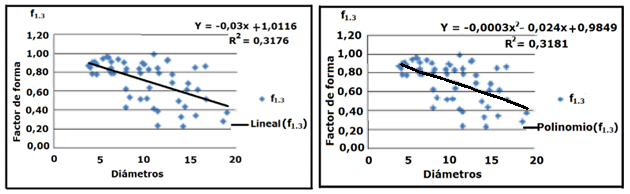
Figura 3. - Ecuaciones de mayor correlación f1,3/d1,3 sin agrupar en clases diamétricas
Pero la representación gráfica de la correlación f1,3/d1,3 se ajusta mejor a la ecuación de un polinomio de segundo grado.
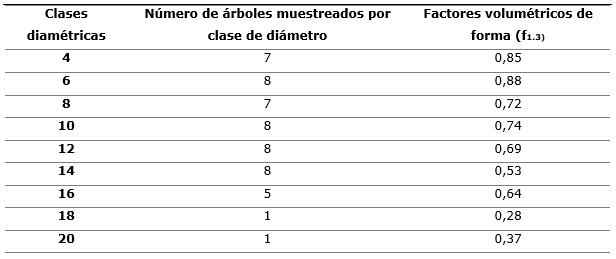
En la Tabla 2, se resumen los valores medio de f1,3 agrupado en clases diamétricas y también se muestra una clara tendencia decreciente con el aumento de los diámetros. Pero a partir de la clase de diámetro 12 los valores medio de f1,3 son menores que el valor medio de f1,3 = 0,71 sin agrupar.
Tabla 2. - Factor volumétrico (f1,3) medio y por clases diamétricas para Brachystegia floribunda
La Figura 4 presenta también las ecuaciones de correlación f1,3/d1,3 y las tendencias de f1,3 respecto a los diámetros y el valor de R2 agrupados en clases diamétricas, con los mismos tipos de ecuaciones considerados anteriormente, sin agrupamiento de los valores de f1,3 por clases diamétricas.
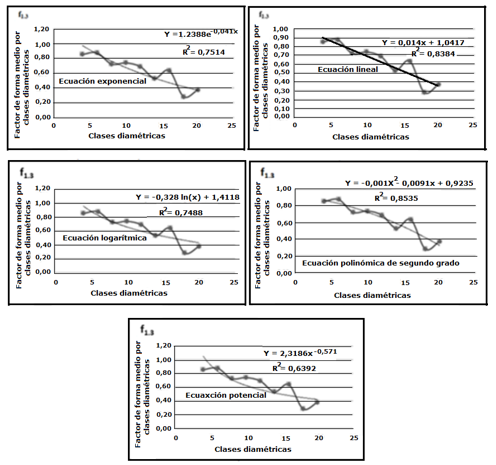
Figura 4. - Ecuaciones de correlación f1,3/d1,3 agrupados en clases diamétricas
Aquí se muestra una tendencia decreciente más acentuada de f1,3/d1,3 y el coeficiente de determinación es más alto que cuando no se agrupan los valores de f1,3 en clases diamétricas, lo que indica que la correlación f1,3/d1,3 es mayor cuando se agrupan en clases diamétricas. Aquí la mayor correlación está también en las ecuaciones lineal con un R2 = 0,8384 y la ecuación polinómica de segundo grado con un R2 = 0,8535, superior a la ecuación lineal. Por tanto, la representación gráfica de la correlación f1,3/d1,3 agrupados en clases se ajusta mejor a la ecuación de un polinomio de segundo grado.
Validación del factor volumétrico de forma del fuste de B. floribunda
En la Tabla 3, están los estadísticos de validación de ambos factores de forma agrupados y sin agrupar). Aunque ambos R2 son bajos, fue el volumen estimado con el factor de forma con los árboles agrupados el que mostró mayor coeficiente de determinación (R2 = 0,46267). También el menor error estándar estimado (EEE = 0,02654) se consiguió con f1,3 = 0,63 agrupado en clases de diámetros y registró un sesgo negativo bajo, por tanto, es recomendable la utilización como factor de forma para la estimación de los volúmenes de árboles en pie de B. floribunda, los agrupados en clases diamétricas.
Tabla 3. - Estadísticos de validación de los f1,3 de B. floribunda
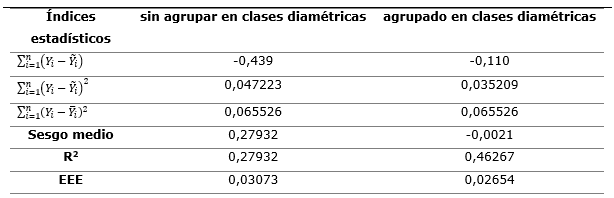
Por tanto, el factor volumétrico de forma que debe emplearse, preliminarmente, para la estimación del volumen del fuste de la especie B. floribunda será tomado de la Tabla 2 para cada una de las clases diamétricas.
Cociente de forma del fuste de B. floribunda
Conforme muestra la Figura 5, no hay una tendencia marcada de variación del cociente de forma respecto a los diámetros, indicando también una baja correlación QS/d.
El cociente de forma medio (QS) sin agrupamiento de los árboles por clases diamétricas, conforme se muestra al final de la última columna de la Tabla 1, es 0,70; similar al valor del factor volumétrico de forma que es 0,71.
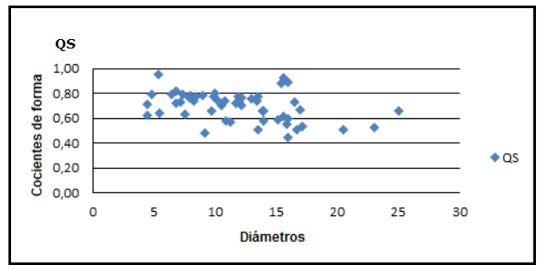
Figura 5. - Dispersión del factor diamétrico de forma o cociente de forma (QS) respecto a los diámetros sin agrupar
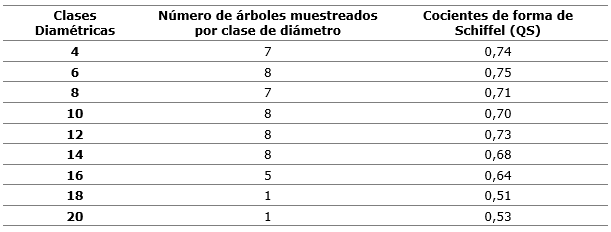
La Tabla 4 muestra los valores de QS cuando los árboles se agrupan en clases diamétricas, donde se observa una tendencia de disminución con el aumento del diámetro. Esta tendencia se corresponde con la que muestra el factor volumétrico de forma del fuste, lo que significa que, aunque existe una diferencia en valores de 0,04, en la práctica son equivalentes.
Tabla 4. - Cocientes de forma del fuste de Brachystegia floribunda Benth según clases diamétricas
La Figura 6 muestra la ecuación que define la tendencia de los cocientes de forma respecto al diámetro.
La ecuación corresponde a un polinomio de segundo grado con una alta correlación de 0,945 y un coeficiente de determinada de R2=0,894, también alto.
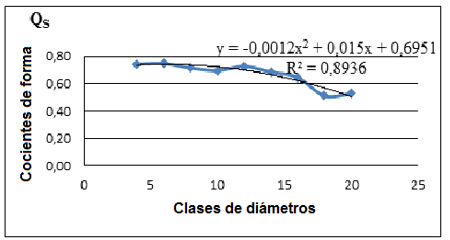
Figura 6. - Correlación (QS/d1, 3) de los cocientes de forma de B. floribunda respecto a las clases diamétricas
Factor volumétrico de forma de las ramas de B. floribunda
En la Tabla 5, también se muestra un esquema de la base de datos con algunos valores, donde se indican las principales variables dendrométricas que se midieron en cada una se las ramas evaluadas. En las tres últimas columnas, aparecen los factores de formas tomando diámetros de referencias en la base a 0,3 m de la base y a 1,0 m de la base.
Tabla 5. - Variables dendrométricas y factores de forma de las ramas de B. floribunda
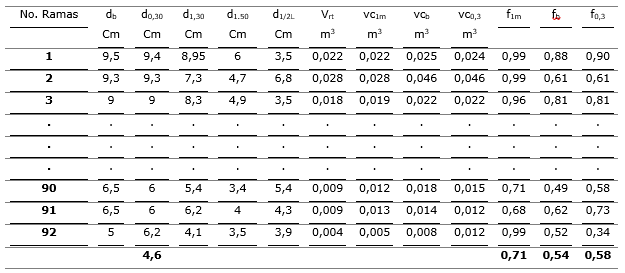
Los factores de forma fb y f0,3 son los que mayor dispersión muestran. Los valores medios de los factores de forma de las ramas sin agrupar son: fb = 0,54; f0,3 = 0,58 e f1m =0,71.
En la Tabla 6, se muestran los resultados de los factores de forma con los mismos diámetros de referencias, pero agrupados en clase de longitud de las ramas.
Tabla 6. - Factores de forma de las ramas de Brachystegia floribunda según clase de longitud
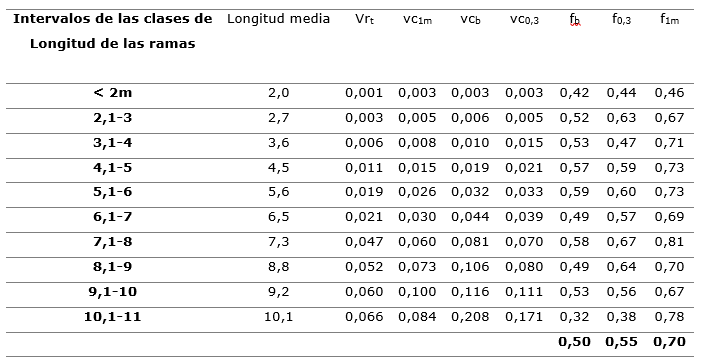
En este caso, los factores de forma agrupados en clases de longitud son: fb = 0,50; f0,3 = 0,55 y f1m =0,70 respectivamente y fueron obtenidos, a partir de la rama que tiene la longitud media del intervalo o rango de todos los árboles de dicho intervalo de clase.
La Figura 7 muestra la correlación de los factores de forma de las ramas respecto a las longitudes de las mismas sin agrupar y agrupada.
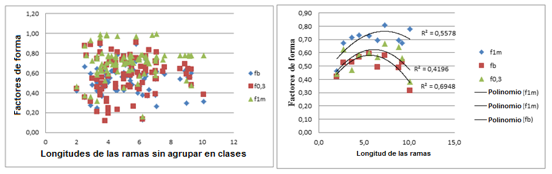
Figura 7. - Factores de forma de las ramas con diferente diámetro de referencia
El factor de forma de las ramas crece con la altura del diámetro de referencia; lo mismo sucede cuando se agrupan en clases de longitudes. Además, aumentan con la longitud hasta alrededor de los 6 o 7 metros, a partir de la cual comienza a disminuir.
La ecuación que mejor define la línea de tendencia y la que más alta correlación mostró entre los respectivos factores de forma y la longitud de las ramas fue el polinomio de segundo grado; fb fue el de mayor correlación con la longitud de las ramas con un coeficiente de determinación de R2=0,6948.
También se evaluaron los factores de forma de las ramas agrupándolos por clases de diámetros (Tabla 7). En este caso los valores obtenidos fueron: fb = 0,53; f0,3 = 0,54 y f1m =0,69
Tabla 7. - Factores de forma de las ramas con relación al diámetro agrupado en clases diamétricas
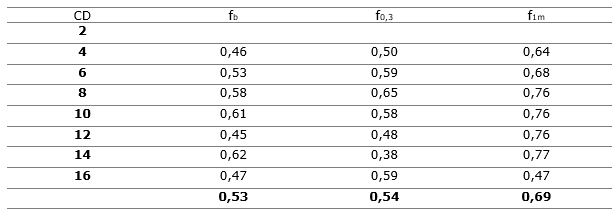
Conforme muestra la Figura 8, los factores de forma agrupados en clases de diámetros, son similares a los obtenidos cuando se agrupan en clases de longitud, excepto el factor de forma en la base (fb) que es superior, mientras (f0,3) y (f1m) son ligeramente inferiores.
En la Figura 8 se muestran las tendencias y los coeficientes de determinación de los tres factores de forma de las ramas con relación a las clases diamétricas.
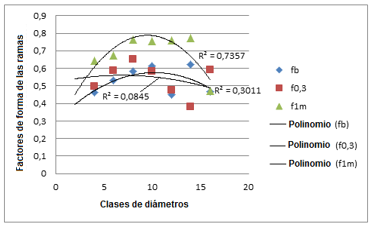
Figura 8. - Correlación factores de forma de las ramas con la longitud agrupadas en clases diamétricas
Las ecuaciones de las tres líneas de tendencias también se corresponden con un polinomio de segundo grado y también fb fue la que mayor correlación muestra, con un coeficiente de determinación de 0,736, superior al valor cuando se agrupan los factores de forma en clases de longitud.
En general, se observa que, mientras en el fuste el factor de forma disminuye con el aumento del diámetro; en la rama tiene la tendencia a aumentar con el diámetro hasta aproximadamente los 10 cm y a partir de ahí comienza a disminuir, es decir que la forma de las ramas tiende más a la forma del paraboloide.
Validación de los factores volumétricos de forma de las ramas de la especie.
Brachystegia floribunda
Un análisis de los índices estadísticos permitió evaluar con mayor precisión el mejor factor de forma medio para la estimación del volumen de las ramas de Brachystegia floribunda.
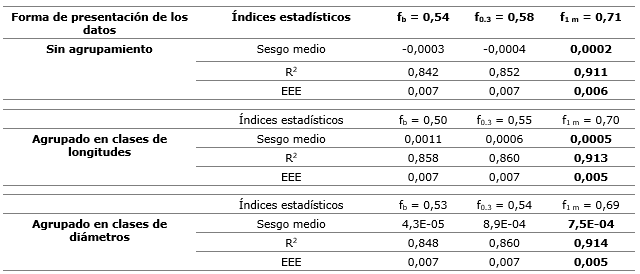
En la Tabla 8, se observa que el factor de forma medio calculado con el diámetro de referencia a 1 m de la base de la rama fue el de mayor correlación con la longitud de las ramas y con los diámetros sin agrupar, pero los mejores resultados se obtuvieron cuando las ramas se agrupan en clases de longitudes o diamétricas, no mostrando prácticamente diferencia entre ambas formas de agrupamientos de las ramas. Por tanto, para la estimación del volumen de las ramas en la especie Brachystegia floribunda se recomienda medir el diámetro de referencia para calcular el volumen del cilindro a 1 m de la base de las ramas y multiplicar este volumen por el factor de forma de 0,7.
Tabla 8. - Estadísticos de validación de los tres factores de forma (fb), (f0.3) y (f1) de la rama de Brachystegia floribunda
CONCLUSIONES
Existe una correlación entre el factor de forma y el diámetro, siendo mayor cuando los árboles se agrupan en clases de diámetros.
El factor de forma disminuye con el aumento del diámetro, ajustándose a una ecuación polinómica de segundo grado, pero el valor recomendable debe ser para cada clase de diámetro cuando los árboles se agrupan en clases de diámetros.
El factor de forma de la rama de Brachystegia floribunda tiene tendencia a aumentar con la altura del diámetro de referencia y de la longitud de las ramas hasta aproximadamente los 10 cm de diámetro y hasta alrededor de los 6 o 7 metros de longitud a partir del cual comienza a disminuir.
Para la estimación del volumen de las ramas de Brachystegia floribunda se debe medir el diámetro de referencia para calcular el volumen del cilindro a 1 m de la base de las ramas y multiplicar este volumen por el factor de forma de 0,69.
El valor medio del cociente de forma calculado sin agrupamiento de los árboles por clases diamétricas es de 0,70 similar al valor del factor volumétrico de forma.
Se recomienda para la estimación del volumen, emplear el cociente de forma que corresponde a la clase diamétrica del árbol.
REFERENCIAS BIBLIOGRÁFICAS
ALBUQUERQUE SARDINHA, R.M. de, 2008. Estado, dinâmica e instrumentos de política para o desenvolvimento dos recursos lenhosos no município da Ecunha, Angola [en línea]. Angola: IMVF - Instituto Marquês de Valle Flôr. [Consulta: 3 septiembre 2020]. Disponible en: https://pdfslide.net/documents/desenvolvimento-dos-recursos-lenhosos-ecunha.html.
CAETANO, T.P., 2012. Perfil forestal de Angola. 1o Congresso dos Engenheiros de Língua Portuguesa. Angola: s.n.
CASTANHEIRA DINIZ, A., 1973. Características mesológicas de Angola: descrição e correlação dos aspectos fisiográficos, dos solos e da vegetação das zonas agrícolas angolanas [en línea]. Angola: Missão de Inquéritos Agrícolas de Angola. ISBN 972-8975-02-3. Disponible en: https://books.google.com.cu/books/about/Caracter%C3%ADsticas_mesol%C3%B3gicas_de_Angola.html?id=f -c6AAAAMAAJ&redir_esc=y.
OLIVEIRA, A.D. de, DEHON, G., SCOLFORO, J.R. y THIERSCH, C.R., 2006. Acurácia dos métodos para estimación do volume comercial de clones d e Eucalyptus sp. Cerne, Lavras [en Línea], vol. 12, no. 2, pp. 167-181. [Consulta: 3 septiembre 2020]. Disponible en: https://www.researchgate.net/publication/237039557_Acuracia_dos_metodos_para_estimación_do_volume_comercial_de_clones_de_Eucalyptus_sp.
PÉLLICO NETTO, S., 2004. Equivalência volumétrica: uma nova metodologia para estimación do volume de árvores. Revista Acadêmica: ciências agrárias e ambientais, vol. 2, no. 1, pp. 17-30.
SANFILIPPO, M., 2014. Trinta árvores e arbustos do Miombo Angolano. Guia de campo para a identificação [en línea]. Angola: ONG COSPE (Cooperazione per lo Sviluppo ei Paesi Emergenti). [Consulta: 3 septiembre 2020]. Disponible en: https://www.academia.edu/17163898/Trinta_%C3%A1rvores_e_arbustos_do_miombo_Angolano_Guia_de_campo_para_a_identifica%C3%A7%C3%A3o.
THOMAS, C., ANDRADE, C.M., SCHNEIDER, P.R. y GUIMARÃES FINGE, C.A., 2006. Comparação de equações volumétricas ajustadas com dados de cubagem e análise de tronco. Ciencia Florestal Santa Maria [en línea], vol. 16, no. 3, pp. 319-327. [Consulta: 3 septiembre 2020]. ISSN 0103-9954. DOI 10.5902/198050981911. Disponible en: https://www.researchgate.net/publication/27790615_Comparacao_de_equacoes_volumetricas_ajustadas_com_dados_de_cubagem_e_analise_de_tronco.
WYK, B. Van, 2013. Field Guide to Trees of Southern Africa [en línea]. South Africa: Penguin Random House South Africa. ISBN 978-1-77584-104-3. Disponible en: https://books.google.com.cu/books/about/Field_Guide_to_Trees_of_Southern_Africa.html?id=dw1bDwAAQBAJ&redir_esc=y.
Conflicto de intereses:
Los autores declaran no tener conflictos de intereses.
Contribución de los autores:
Edilio Aldana Pereira: Concepción de la idea, búsqueda y revisión de literatura, confección de instrumentos, aplicación de instrumentos, recopilación de la información resultado de los instrumentos aplicados, análisis estadístico, confección de tablas, gráficos e imágenes, confección de base de datos, asesoramiento general por la temática abordada, redacción del original (primera versión), revisión y versión final del artículo, corrección del artículo, coordinador de la autoría, traducción de términos o información obtenida, revisión de la aplicación de la norma bibliográfica aplicada.
Yordan Lores Pérez: Concepción de la idea, búsqueda y revisión de literatura, confección de instrumentos, aplicación de instrumentos, recopilación de la información resultado de los instrumentos aplicados, análisis estadístico, confección de tablas, gráficos e imágenes, confección de base de datos, asesoramiento general por la temática abordada, redacción del original (primera versión), revisión y versión final del artículo, corrección del artículo, coordinador de la autoría, traducción de términos o información obtenida, revisión de la aplicación de la norma bibliográfica aplicada.
![]()
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial
4.0 Internacional.
Copyright (c) 2021 Edilio Aldana Pereira, Yordan Lores Pérez.